An Easy Structure - Sucrose

1/6) Space group determination - XPREP

The SHELXTL software includes a very useful utility called XPREP. In this example, XPREP is used to determine the space group, and to prepare an input file to solve the structure. XPREP has a bunch of other uses, but we will ignore them for now. Much of the following is done from a command line. While this may seem archaic, once you become familiar with typing commands you will find that it is much faster and much more direct than blundering through a graphical interface. To proceed on linux or on a Mac you should have your '*.hkl' and '*.html' files ready and a terminal (e.g. xterm or similar) window open, i.e. something like this:

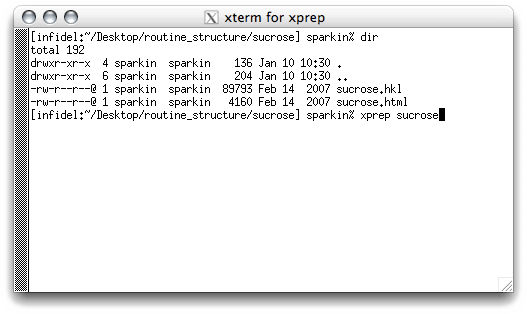
To start XPREP, simply type 'xprep sucrose' at the prompt and hit the <return> key. If your '*.hkl' file is not named 'sucrose', then you need to use that filename instead of 'sucrose'. The program is smart enough to look for a file with the '.hkl' extension. This will give you something like this:

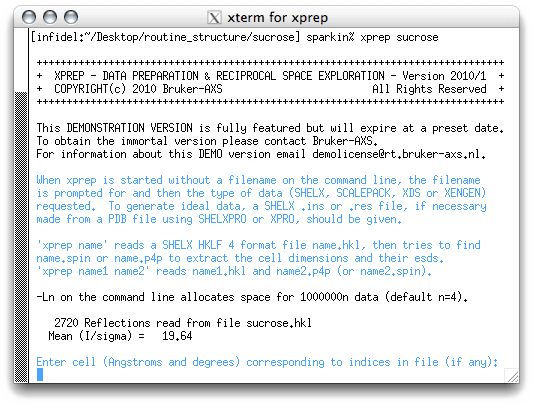
To enter the cell dimensions you simply type them in. As stated above, the best estimates of the cell dimensions available from data collected on the kappaCCD are contained in the nreport.html file, which is a summary of data collection, scaling and merging statistics. Since it is an ordinary html file, it can be read with a web browser or with a text editor. To open it with (say) firefox, then type 'firefox filename.html' (again, substitute the proper filename here!). It looks something like this:

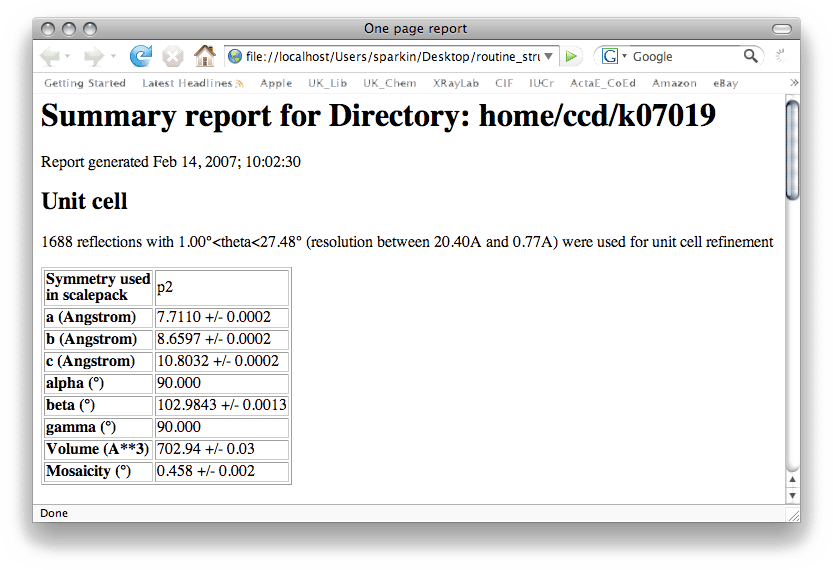
You may notice the filename given at the top of this nreport.html (k07019) is different from the filename we are using (sucrose). Renaming to 'sucrose' was just for the sake of convenience. The k07019 name follows the convention used in the X-ray lab. at UK (k = kappaCCD, 07 = the year 2007, 019 = the 19^th data collection done that year). You can of course use whatever filename you like, but it helps with bookkeeping if you follow some sort of convention.

It is always best practice to keep good notes. This is especially true for novices, so write these numbers down in your notebook! Also make note of the uncertainties that are associated with each of the cell dimensions. You will need these later (vide infra). In any event, type the cell dimensions into XPREP, all on one line and separated by spaces like this:

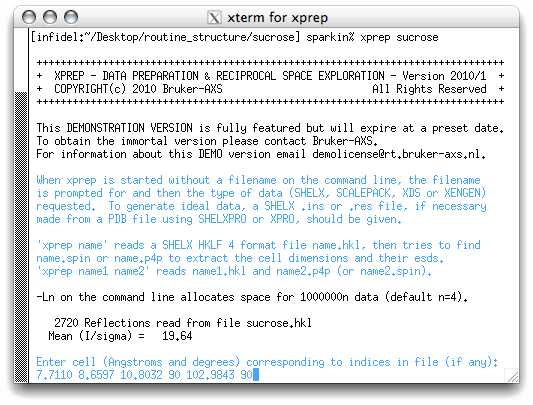
When you hit <return> you will get the following:

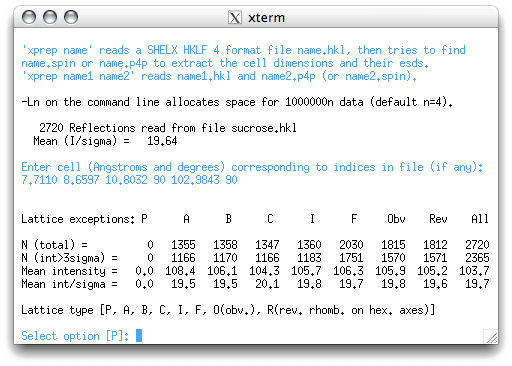
One of the great things about XPREP is that it usually makes sensible choices. Nevertheless, it helps to know what is going on. The table in the window above allows you to tell the program whether the crystal has a primitive or a centered unit cell. If you don't know what that means, consult your notes or an introductory textbook.

So, how to read this table? Notice there is a column for P (primitive), as well as columns for various centering conditions (A,B,C etc.). Below these labels there are numbers that tell you how often a particular criterion is violated. Since it is always possible to fit a primitive lattice to a set of regularly-repeating points in 3D space, there should always be a bunch of zeroes in the P column. The other columns have non-zero numbers in them. If the unit cell was centered, then it would be apparent from the numbers in these columns. For example, if the lattice was really I-centered (the I means body centered, and is from the German innenzentriert), then the intensity found for any reciprocal lattice point with an odd number for h+k+l, would be negligible. In the table this would give small numbers in the I column for the bottom two rows.

XPREP usually makes the right choice, and gives its best guess in square brackets. Since the cell is indeed primitive, all you have to do is hit <return>. This brings up the main XPREP menu:

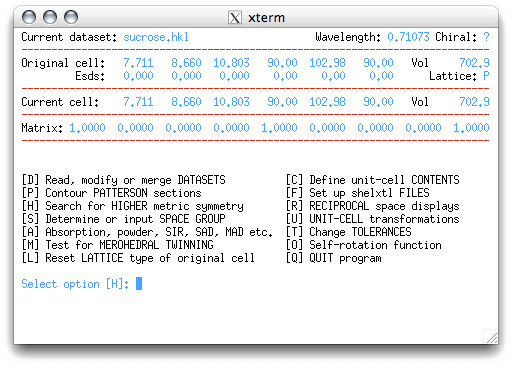
In this example, we will only use a small subset of the tools available in XPREP. If you feel the need to try the other features, go ahead. Some of these will be used in later tutorials for more difficult structures.

XPREP suggests the option H, which will search for a higher-symmetry cell. When you hit <return>, the program responds like this:

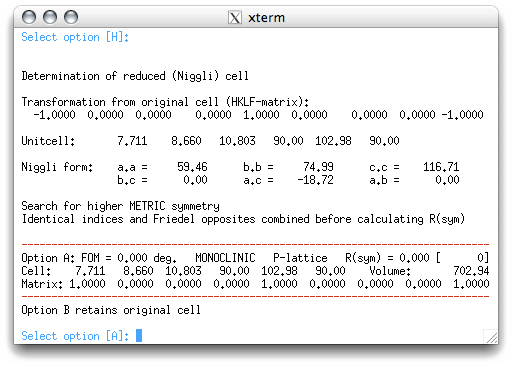
In this example, the program suggests a cell that is identical to the one you typed in. It also gives a second option that retains the original cell. In this case, options A and B are the same. More complicated structures might give a few different possibilities for you to consider. In this case, however, the program is not able to find a higher symmetry cell, so we accept the default value by hitting <return>. This sends us back to the main menu, which now suggests the "S" option for space group determination:

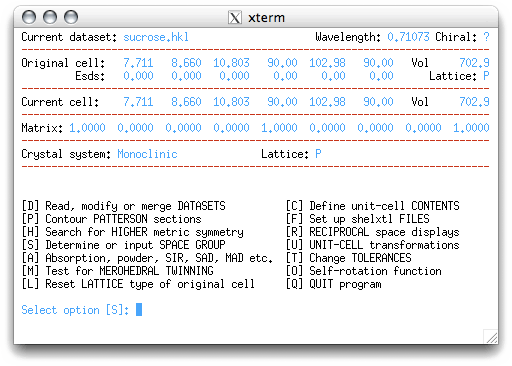
Do the obvious thing, hit <return> to get this:

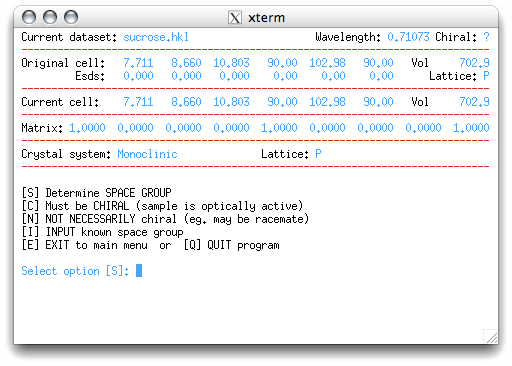
If you know the space group already, you could enter 'I' at the prompt. Since we know that sucrose is chiral, we could enter that here, but let's make the program do all the work! Go ahead and enter 'S', as suggested by XPREP:

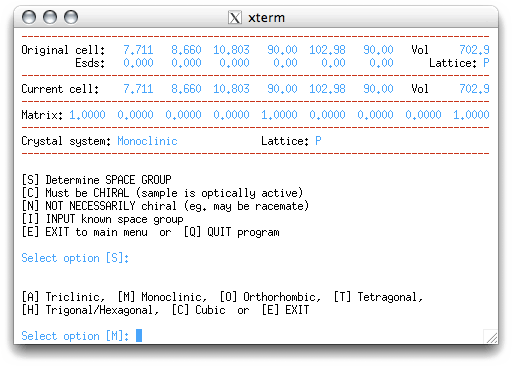
To proceed, the program needs to know the crystal system. It can usually figure this out from the metrics of the cell, but there are cases where it can be deceived, e.g. for a monoclinic crystal with β=90° it will suggest orthorhombic. Here it makes the correct choice of monoclinic, so accept the default value of 'M' by hitting <return>.

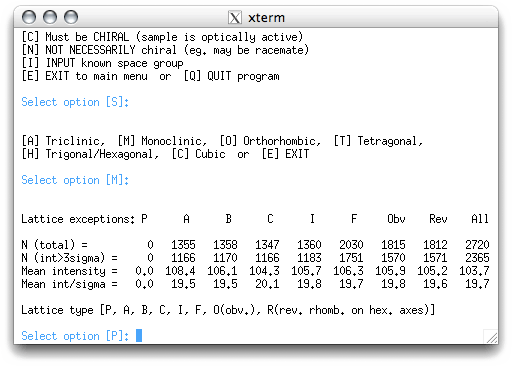
Here the program gives you a chance to revise your choice of centering, but it is unusual that you'd want to change this. In this case, you know it is primitive, so accept 'P' by hitting <return>, which gives:

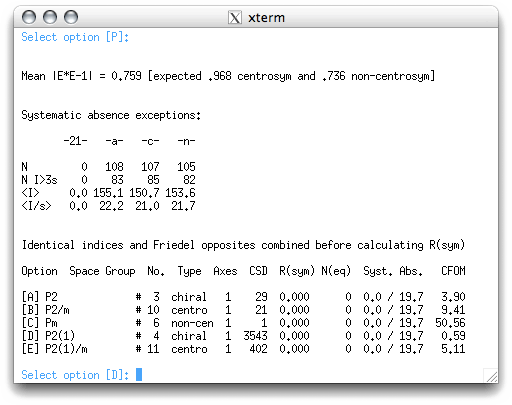
Here we get three blocks of information:

The mean |E*E-1| statistic gives information on whether the structure is likely to be centrosymmetric or non-centrosymmetric. All it does is to compare the value calculated for the dataset (0.759) with a theoretical value for centrosymmetric (0.968) and non-centrosymmetric (0.736) intensity distributions. Here it is clear that the sucrose data are non-centrosymmetric, and this makes sense. Sucrose molecules are chiral, and at least with naturally occuring sucrose there is only one enantiomer. This means that it has to be non-centrosymmetric. This statistic must be treated with caution because it can be misleading. Examples of such problems usually involve data from twinned crystals, pseudo-symmetric crystals, non-centrosymmetric crystals that happen to have centrosymmetric distributions of heavy atoms etc. None of those problems concern us here because the |E*E-1| value is reasonable.

The next block tells us about the presence of screw axes (written as -21- in the table column heading) and glide planes (written as -a-, -c-, -n-). The table is laid out in much the same way as the table used to decide on the presence of lattice centering. In this example there are no violations for the 2₁ screw axis, but plenty of violations for the a,c,n glide planes. Again, this makes complete sense. Since natural sucrose has just one enantiomer, there can't possibly be any glide planes in the crystal structure because glide planes include a mirror operation. Note: depending on how the data reduction was performed, there may have been non-zero numbers in the 2₁ column. This would happen if the systematically absent reflections were left in the dataset during merging and scaling. If you don't know what this means, you may want to find out. Either way, it should be apparent that there is a 2₁ screw axis in this structure.

XPREP uses all the information gathered so far to try to ascertain the space group. There are usually a few suggestions along with a bunch of information that enable you to make an informed choice. Probably the most useful statistic here is the CFOM (combined figure-of-merit), which is usually smallest for the correct space group. In this case, XPREP suggests option 'D', P2(1), which is just the SHELX way of writing P2₁. Accept this by hitting <return>.

We're back at the main menu, but with the 'D' option recommended as the next step. In this tutorial we will simply hit the <return> key through these screens, but a brief explanation of each will be given:

This is a separate sub-menu. The program wants to show you some intensity statistics, hit <return>.

Merging and intensity statistics depend on whether symmetry equivalents have been merged or not. Feel free to try the different options. If you try the suggested 'A' option you get the following:

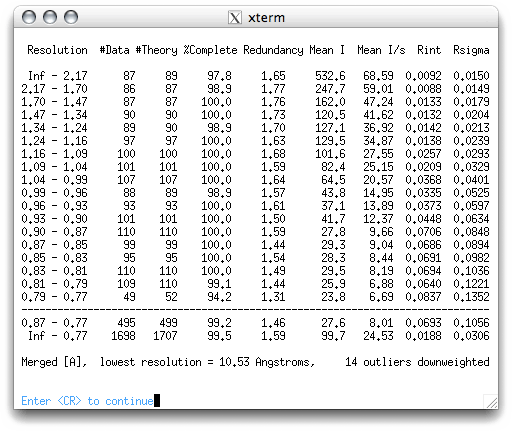
As you can see, there's a lot of information. The table splits the data into resolution shells with roughly the same number of reflections in each. The R_int column gives a measure of whether symmetry equivalents have the same intensity. Notice that in the higher resolution shells (lower down the table), the R_int values get larger. The mean intensity and mean I/sigma tend to get smaller at higher resolution, while the R_sigma get larger. These variations with resolution happen because diffraction intensities tend to be weaker, and therefore more susceptible to noise, at higher resolution. As a general rule, the data are usable so long as the mean I/σ for a shell is >2 and the Rint < 0.3, but there is some leeway. There is little point in including very high-resolution reflections if all they contain is noise, so you may occasionally have to truncate the high-resolution limit a bit (seek help if you are unsure). In any event, this sucrose data is strong throughout the whole resolution range.

On hitting <return> we get the following.

This sends us back to the main menu:

The 'C' menu item allows us to enter the molecular formula:

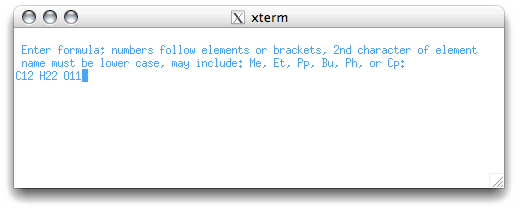
It is not absolutely necessary to know the formula, but it does help. If you don't know it, you can make up something plausible based on what the starting materials were, but remember to correct it later! When a formula is entered you get a chance to change some other stuff, as follows.

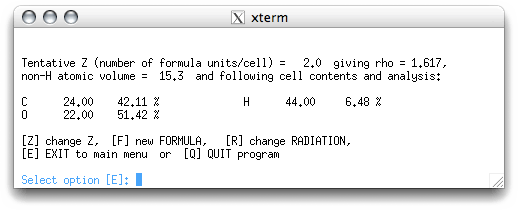
The Z value is the number of formula units in the unit cell. The program estimates Z based on the formula and the unit cell volume. If you have the formula correct, this is usually a good estimate. On returning to the main menu, you get this:

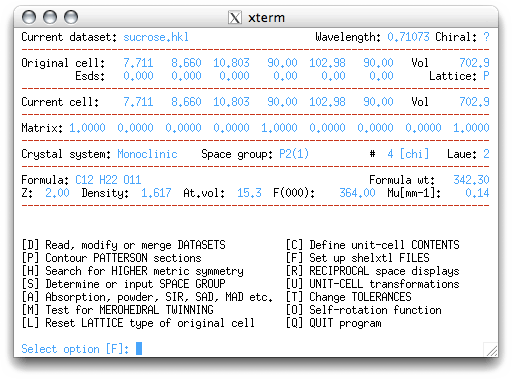
The next menu item selected is 'F', which sets up the files to be used by SHELXS, the structure determination program. On hitting <return>, you get to choose the filename for your instructions ('.ins') file:

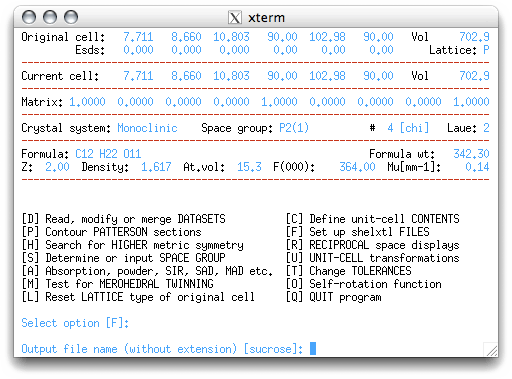
For a routine structure it is ok to keep the same file name, but in some circumstances you may need to change it. This could happen if you had to re-index your data for any reason, e.g. if you found a higher symmetry cell. Here we choose the default 'sucrose', by hitting <return>. You get a choice of whether to use SHELXS (most common) or SHELXD (mainly for difficult cases). There is now a third option, SHELXT, which will work with files created for either SHELXS or SHELXD.

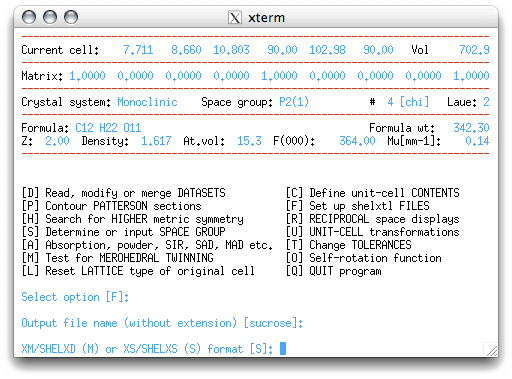
For this example, choose 'S' for SHELXS, to get:

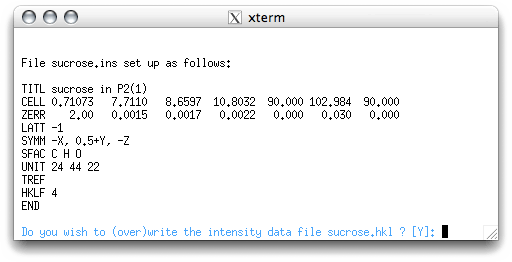
XPREP gives you a listing of the instructions file ('sucrose.ins'), and the option of writing (or overwriting) the data file. You may recognize some of the numbers given here. The numbers on the CELL line are the wavelength of the X-rays in ångstrom units, followed by the cell dimensions. On the ZERR line below CELL, the numbers are Z (i.e., the number of formula units) followed by standard uncertainties (SU values) for each of the cell parameters. Unfortunately for kappaCCD data, the SUs written by XPREP are incorrect. The proper values are given in the nreport.html file, which means you will have to manually edit the '.ins' file to enter the proper values (you'll do this next). The rest of the commands in the '.ins' file will be explained in the next section of this tutorial. You are now ready to quit XPREP and solve the structure, so hit <return>.

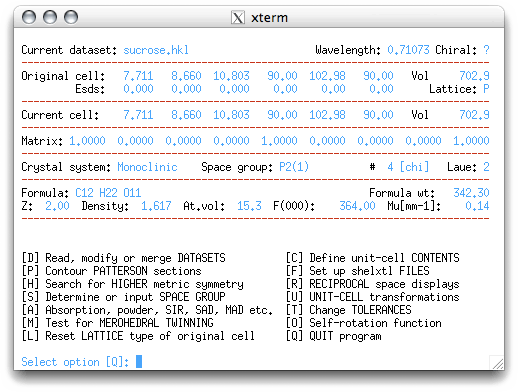
This sends you back to the command line of the terminal window. If you want to see what files XPREP has created, type 'dir' and hit <return> (note: the 'dir' command is used in the UK X-ray lab. as a shorthand alias for the unix command 'ls -l', so it may not be present on unix systems outside this X-ray lab.).

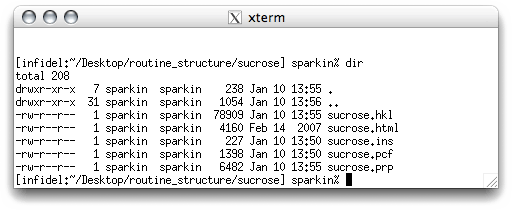
There should be three new files, sucrose.ins, sucrose.pcf, sucrose.prp. As stated above, sucrose.ins contains instructions for the structure solving program, SHELXS. The file sucrose.prp contains a listing of all the stuff that was written to the screen by XPREP, which can be useful for diagnostic purposes. The file sucrose.pcf contains a bunch of information written in CIF format. Note: for data collected on the kappaCCD, not all of the information in the .pcf file is correct, but you do not need to worry about that.