A three-fold twin in B2₁

5/7: Analyze detwinned data using XPREP

When the detwinned dataset is read into XPREP, we get:

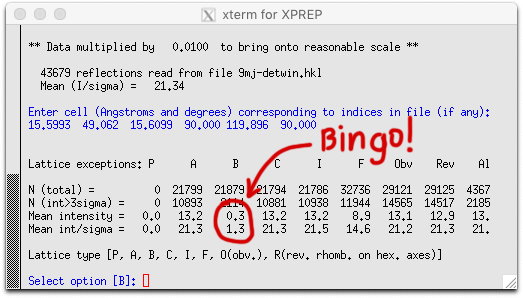
The important things to note here are the 'mean intensity' and 'int/sigma' in the 'B' column. The numbers are tiny, which means that the unit cell with a ≈ c and β ≈ 120° is B-centered, not primitive.

Although it would be trivial to pare down our P2₁ model for B2₁, we'll take the lazy route and re-solve the structure using a B-centered cell. We'll get to that in the last section. In the meantime, the B-centered cell must be equivalent to some primitive cell with half the volume. Before quitting XPREP, let's see what it suggests. A search for higher metric symmetry gives this:

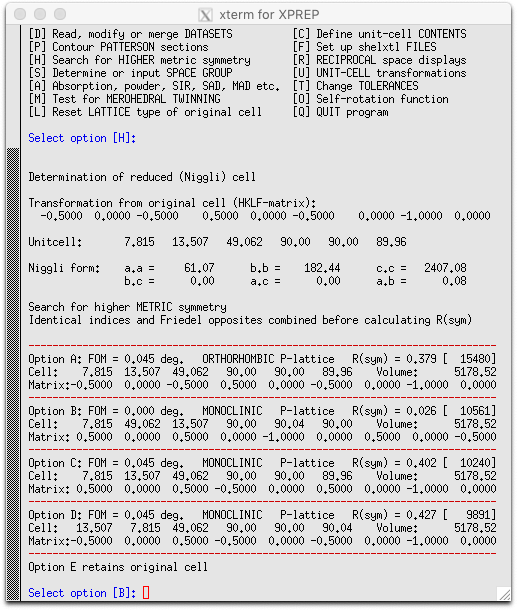
XPREP finds four clearly related cells. They all have the long ~49Å axis, one axis that is half as long as the a and c of the pseudo-hexagonal cell, and one axis that is ^√3/₂ times as long. Option A (primitive orthorhombic) can be rejected because it has lousy R(sym). It also finds three primitive monoclinic cells, but only one (option B) has a good R(sym). The transformation matrix for option B is ...


... which gives β = 90.04°. To preserve the handedness, it rotates the cell so that b points in the opposite direction. Out of curiosity, let's see what XPREP suggests for the space group:

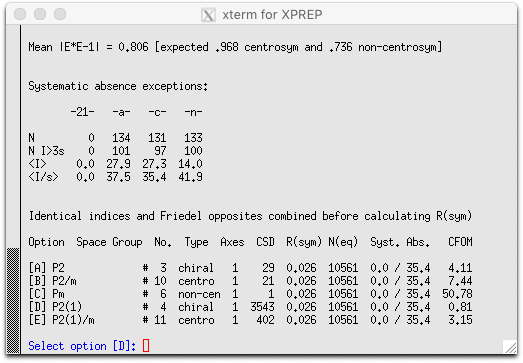
Perhaps not surprisingly, it suggests P2₁. The obvious question then is, why bother with an unconventional B-centered cell if the untwinned structure has a smaller pseudo-orthorhombic primitive monoclinic cell ? The answer lies in the way that SHELXL uses the TWIN instruction. In the B-centered setting, the same TWIN matrix can be applied twice for the 2nd and 3rd components. Three-fold twinning for a pseudo-orthorhombic primitive monoclinic model using SHELXL, however, would require 'HKLF 5' format data, which would obscure the three-fold nature of the twinning, as we'll see in the next section.