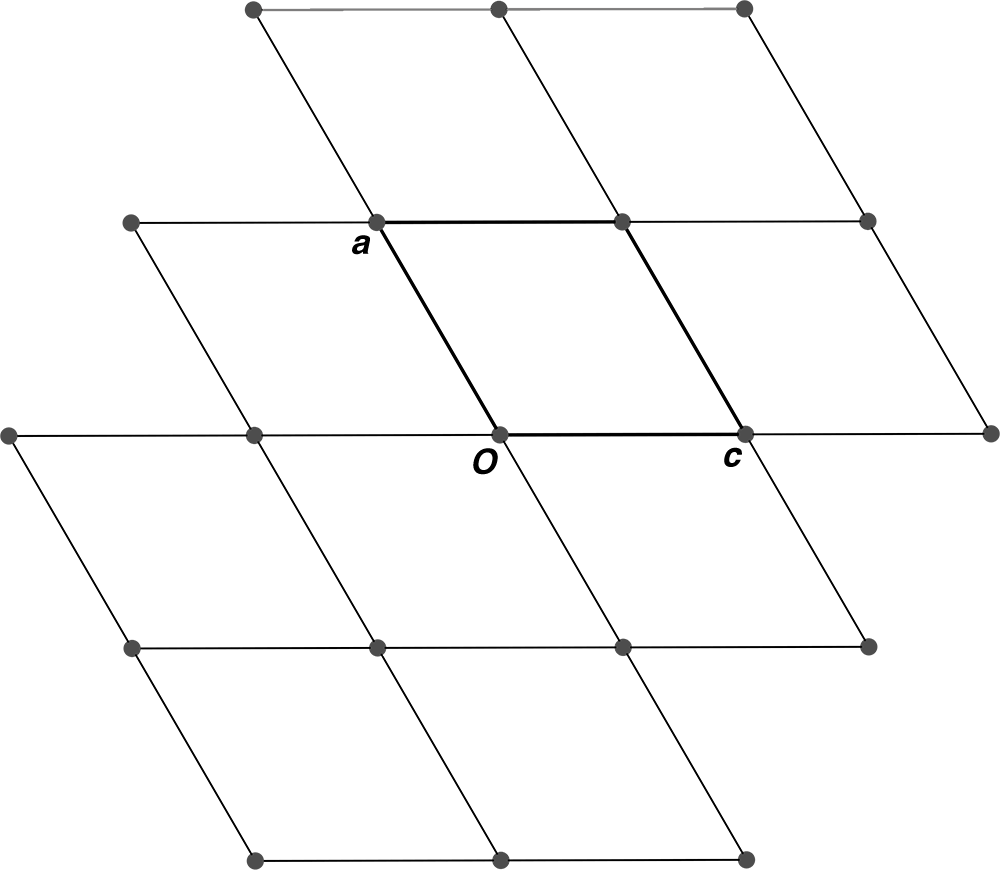
Three-fold twinning about b entails repeated rotation of 120°. A positive
rotation (anti-clockwise), first gives this:

... and then this:

Lattice points for these three orientations exactly superimpose provided a
and c are identical and β is exactly 120°:

Any small deviation causes a slight mis-match in the superposition, which might look something
like this:
For the sake of simplicity, we'll assume that the superposition is exact. Following the notation
used in the International Tables, vol A, chapter 5.1, the cell defined by the row vector
(a,b,c) maps onto (a',b',c') via an anticlockwise rotation,
by a matrix ...
... repeated application of this matrix maps (a',b',c') onto (a",b",c") and then (a",b",c") back onto (a,b,c), which completes the cyclic permutation. Such repetition amounts to multiplying the matrix by itself, giving a new matrix:
The new matrix maps (a,b,c) onto (a",b",c") etc., which would cycle around clockwise. If the first matrix operates on the second (or vice versa), then we get the identity matrix:
The SHELXL TWIN instruction handles such cases by allowing repeated application of the same matrix. However, since the matrix used by TWIN operates on a column vector of reflection indices, it needs the transpose of the above matrices. Three-fold twinning for a B-centered cell with β = 120° can be dealt with in exactly the same way.
That's all well and good, but the B-centered setting is unconventional. We saw in the last section that such a cell transforms to a pseudo-orthorhombic primitive monoclinic cell having β ≈ 90° and half the volume. In projection down b, the primitive cell is rectangular. Here is such a cell superimposed on one component of the triply-twinned lattice of B-centered cells:
3+
[010]
[010]
=
-1
0
1
0
1
0
-1
0
0
... repeated application of this matrix maps (a',b',c') onto (a",b",c") and then (a",b",c") back onto (a,b,c), which completes the cyclic permutation. Such repetition amounts to multiplying the matrix by itself, giving a new matrix:
3-
[010]
[010]
=
-1
0
1
0
1
0
-1
0
0
×
-1
0
1
0
1
0
-1
0
0
=
0
0
-1
0
1
0
1
0
-1
The new matrix maps (a,b,c) onto (a",b",c") etc., which would cycle around clockwise. If the first matrix operates on the second (or vice versa), then we get the identity matrix:
-1
0
1
0
1
0
-1
0
0
×
0
0
-1
0
1
0
1
0
-1
=
1
0
0
0
1
0
0
0
1
The SHELXL TWIN instruction handles such cases by allowing repeated application of the same matrix. However, since the matrix used by TWIN operates on a column vector of reflection indices, it needs the transpose of the above matrices. Three-fold twinning for a B-centered cell with β = 120° can be dealt with in exactly the same way.
That's all well and good, but the B-centered setting is unconventional. We saw in the last section that such a cell transforms to a pseudo-orthorhombic primitive monoclinic cell having β ≈ 90° and half the volume. In projection down b, the primitive cell is rectangular. Here is such a cell superimposed on one component of the triply-twinned lattice of B-centered cells:

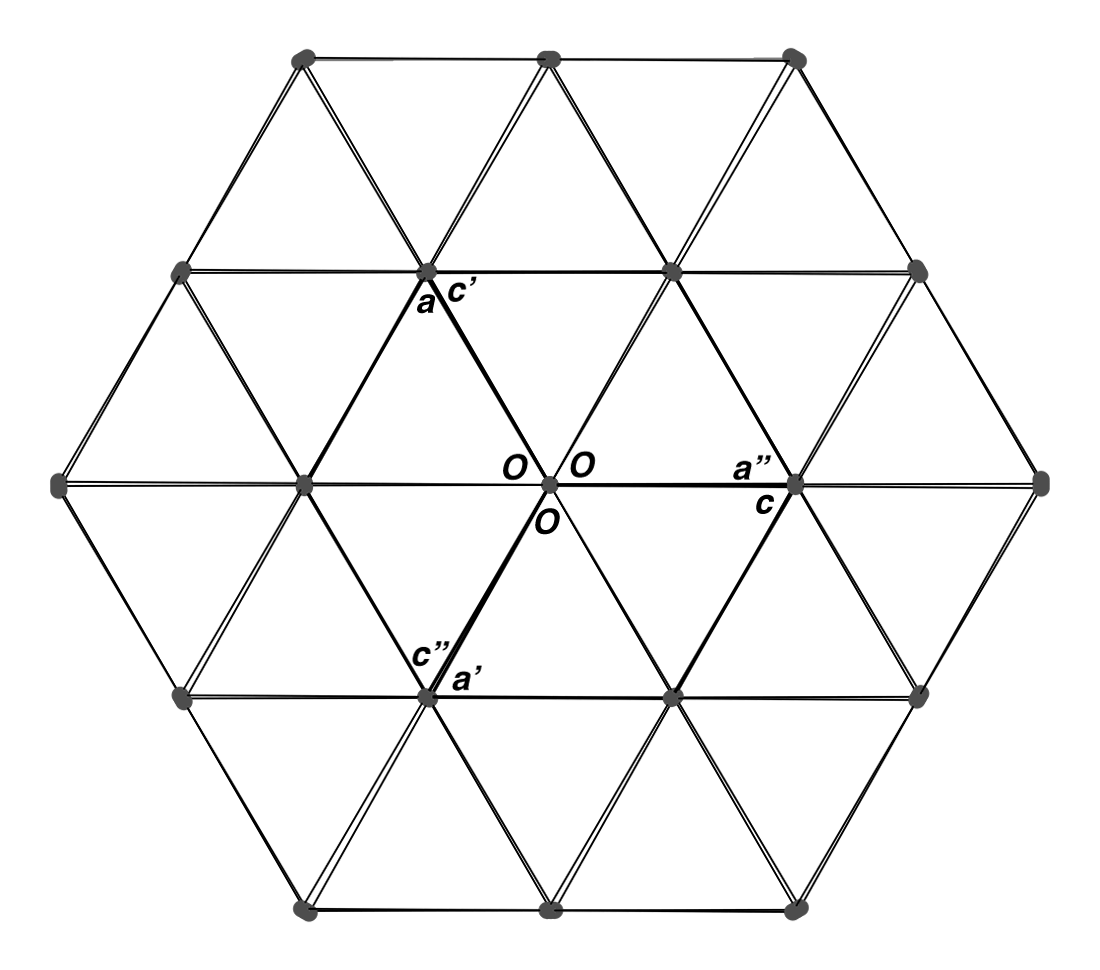
An anti-clockwise rotation of 120° about b looks like this:

While 240° (or -120°) about b gives:

The lattice points in these three twin components are no longer fully superimposable.
Half of them align well, but there are twice as many apparent lattice points in the
(3-fold) twin compared to any individual twin component. Expressed in more rigorous language,
the index of the twin is 2, as illustrated in the following composite image:

If we highlight the primitive cells for each twin component, we get:
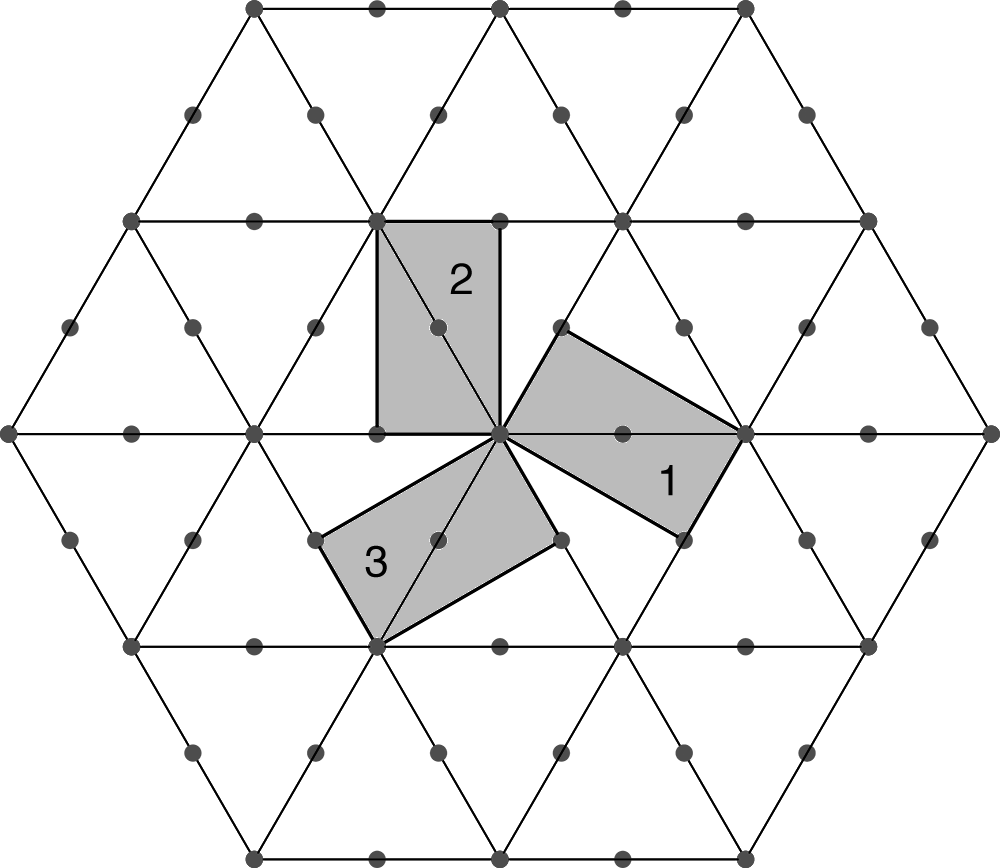
The above diagram appears to imply these rectangular cells are centered, but that is
purely a visual artefact of the superposition. Those dots in the middle of the grey rectangles
represent lattice points of other twin components. For example, the dot in the middle
of cell 1 is a point in the lattice corresponding to cell 2. The individual twin components are
of course, still primitive. As with the B-centered three-fold description, these
primitive cells must also be related by 120° and 240° rotations, but the rotation
matrices are not so obvious because the SHELXL TWIN command operates relative to a single
twin component rather than the twin itself, and it does so in reciprocal space. Thus, TWIN in
SHELXL would map reflections from component 1 onto those of component 2 using the following
rotation matrix:
Analogous to the primitive case (above), repeated application maps diffraction from component 2 onto diffraction from component 3. The net result is equivalent to mapping data from 1 onto data from 3 by the resulting matrix (which describes a clockwise rotation):
As expected, the two matrices operating on each other generate the identity matrix:
Therefore, as with the B-centered case, repeated application leads to cyclic permutation and can go clockwise or anti-clockwise.
So, why can't we simply take one of the primitive cells and rotate it twice ? The problem, as stated above, is that the SHELXL TWIN matrix applies to diffraction from just one twin component rather than the twin itself. The net result (for SHELXL) is that the superposition of the three components gives twice as many lattice points as any single twin component. That is a(nother) manifestation of the twin index being 2. If we wrote an hkl file for the primitive cell using (say) XPREP, it would have half as many data points as the triply-twinned (i.e. full) dataset. As such, it would not have sufficient information to properly describe all three twin components. Alternatively, if we used the full dataset, but transformed it on-the-fly by reading into a SHELX program like this ...
HKLF 4 1 0.5 0 0.5 0 -1 0 0.5 0 -0.5
... again, we'd lose half the data. Reflections with (odd h and even l ) or (even h and odd l ), would be rejected because they'd be assigned non-integer indices upon transformation. This is a limitation of the TWIN instruction in SHELXL. In principle, we could construct a dataset in 'HKLF 5' format with three components. That's tedious, but not difficult. Nevertheless, the use of B21 for 9mj using SHELXL is far more elegant. Luckily, the crystallographic gods don't care about man-made conventions. The 3-fold twinning in 9mj is by reticular pseudo-merohedry, with zero obliquity (the twin axis is coincident with the cell b axis), but non-zero twin misfit (since β is not exactly 120°, twin-related lattice points do not exactly superimpose).
For a more rigorous treatment, please consult Nespolo, Smaha, & Parkin (2020). Acta Cryst. B76, 643-649.
-0.5
0
-0.5
0
1
0
1.5
0
-0.5
Analogous to the primitive case (above), repeated application maps diffraction from component 2 onto diffraction from component 3. The net result is equivalent to mapping data from 1 onto data from 3 by the resulting matrix (which describes a clockwise rotation):
-0.5
0
-0.5
0
1
0
1.5
0
-0.5
×
-0.5
0
-0.5
0
1
0
1.5
0
-0.5
=
-0.5
0
0.5
0
1
0
-1.5
0
-0.5
As expected, the two matrices operating on each other generate the identity matrix:
-0.5
0
-0.5
0
1
0
1.5
0
-0.5
×
-0.5
0
0.5
0
1
0
-1.5
0
-0.5
=
1
0
0
0
1
0
0
0
1
Therefore, as with the B-centered case, repeated application leads to cyclic permutation and can go clockwise or anti-clockwise.
So, why can't we simply take one of the primitive cells and rotate it twice ? The problem, as stated above, is that the SHELXL TWIN matrix applies to diffraction from just one twin component rather than the twin itself. The net result (for SHELXL) is that the superposition of the three components gives twice as many lattice points as any single twin component. That is a(nother) manifestation of the twin index being 2. If we wrote an hkl file for the primitive cell using (say) XPREP, it would have half as many data points as the triply-twinned (i.e. full) dataset. As such, it would not have sufficient information to properly describe all three twin components. Alternatively, if we used the full dataset, but transformed it on-the-fly by reading into a SHELX program like this ...
HKLF 4 1 0.5 0 0.5 0 -1 0 0.5 0 -0.5
... again, we'd lose half the data. Reflections with (odd h and even l ) or (even h and odd l ), would be rejected because they'd be assigned non-integer indices upon transformation. This is a limitation of the TWIN instruction in SHELXL. In principle, we could construct a dataset in 'HKLF 5' format with three components. That's tedious, but not difficult. Nevertheless, the use of B21 for 9mj using SHELXL is far more elegant. Luckily, the crystallographic gods don't care about man-made conventions. The 3-fold twinning in 9mj is by reticular pseudo-merohedry, with zero obliquity (the twin axis is coincident with the cell b axis), but non-zero twin misfit (since β is not exactly 120°, twin-related lattice points do not exactly superimpose).
For a more rigorous treatment, please consult Nespolo, Smaha, & Parkin (2020). Acta Cryst. B76, 643-649.
In the final section, we'll solve the structure from scratch using space group B21.
1: Introduction
2: Set up instructions using XPREP
3: Solve using P21 with SHELXD
4: Detwin using SHELXL
5: Analyze detwinned dataset using XPREP
6: Three-fold twinning in graphic detail
7: Solve using B21 with SHELXD
2: Set up instructions using XPREP
3: Solve using P21 with SHELXD
4: Detwin using SHELXL
5: Analyze detwinned dataset using XPREP
6: Three-fold twinning in graphic detail
7: Solve using B21 with SHELXD