Twinning by Pseudo-Merohedry

3/4) Decipher the twin law

As stated in the introduction, twinning by pseudo-merohedry may occur in crystals where the cell dimensions mimic a higher-symmetry crystal system. Here we have a monoclinic crystal masquerading as orthorhombic by virtue of a β angle that is almost exactly 90°. The question is: what is the twin law, and how do we describe it in a mathematically rigorous way ? The answer in this case lies in the difference between orthorhombic and monoclinic symmetry. For a monoclinic crystal we could have 2-fold rotation, 2₁ screw, mirror, and c-axial or n-diagonal glide planes associated only with the b axis (assuming standard conventions are respected). For orthorhombic, these symmetry elements may be associated with a, b, and c. In reciprocal space, translational parts of screws and glides show up only as systematic absences, so in deciphering the twin law, we need only consider rotation, reflection and inversion. Since our structure is centrosymmetric, that limits us to 2-fold rotation and mirror operations associated with the a and c axes.

A two-fold rotation changes the sign of two indices, while a mirror flips just one sign. The allowable twin operations, expressed as (3x3) transformation matrices, are as follows:

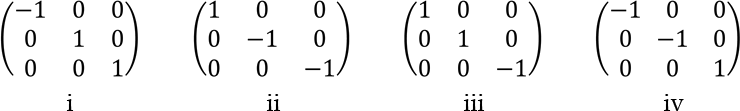
In the above, (i) and (iii) define reflection perpendicular to a and c while (ii) and (iv) describe rotation about a and c, respectively. Since the structure is centrosymmetric, (i) and (ii) are equivalent, as are (iii) and (iv). Similarly, since monoclinic symmetry has either m, 2 or 2/m point symmetry associated with the b axis, we can flip the sign of b (mirror perpendicular to b) or flip the signs of a and c (2-fold about b). Thus (i), (ii), (iii), and (iv) are equivalent: any of the four matrices will accomplish the same result. 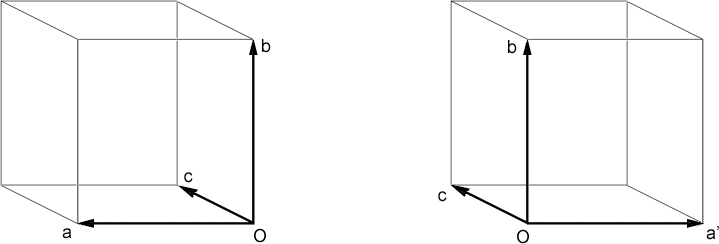To illustrate the superposition of monoclinic twin components when β = 90°, the image below shows two unit cells related by a mirror perpendicular to the a axis.

If you roll your mouse cursor over the image, the unit cell boxes should converge, and exactly superimpose. The superposition is perfect only if bc is perpendicular to a, i.e. if β = 90°. This is the essence of twinning exhibited by the structure in question. The twin components can co-exist side-by-side, with minimal interference or distortion. Without looking at the structure and analysing molecular contacts, however, we cannot tell if the twinning in real space is by a mirror or by 2-fold rotation. We can't even tell which axis is involved, a or c, but for the sake of refinement it doesn't matter: in reciprocal space the four twin operations are equivalent for this crystal. Nevertheless, unless there is some compelling reason to choose otherwise, it makes most sense to use a symmetry operation of the first kind. In other words, choose a proper rotation rather than a reflection (or roto-inversion).

The twin operations given above can be translated into SHELXL commands as follows:

For inclusion in the SHELXL structure model, you should also add a BASF (batch scale factor) instruction with an educated guess at the occupancy factor of the main component. In the final segment, we'll add TWIN and BASF instructions to the model and refine the structure to convergence.